For the classification of base-base interactions, we consider nucleotide pairs that involve at least one of the known chemical stabilizing forces, that is, covalent binding of adjacent bases, H-bond base pairing and base stacking. Base-base interactions are thus of five distinct types: adjacent, adjacent-stacked, adjacent-paired, non-adjacent-stacked and non-adjacent-paired (see Table 3.2). The non-adjacent-non-paired-non-stacked nucleotide pairs are the most frequent, but they were not considered since they do not involve actual chemical interactions.
Traditionnal encodings of adjacent base-base interactions uses the six
backbone torsion angles ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() and
and ![]() [24] or, more recently, the two
pseudotorsion angles
[24] or, more recently, the two
pseudotorsion angles ![]() and
and ![]() [6]. These
parameters accurately describe the relative placement of nucleotides
linked by a phosphodiester bond. However, it has already been
observed that distinct torsion angle combinations can result in
similar backbone directions and base orientations. This phenomenon is
known as the ``crankshaft effect'' [11,22]. Also,
non-adjacent base-base interactions, like base pairings that are
stabilized by H-bonds and non-adjacent base-base stacking, cannot be
accurately parameterized using these angles. Rather, a plethora of
rotation and translation parameters have been used to describe these
interactions [2,15,17]. A simplified
and unified encoding scheme for any type of base-base interactions
that emerged from the introduction of HTMs is introduced. In order to
allow us to effectively compare base-base interactions, a distance
metric between between two HTMs,
[6]. These
parameters accurately describe the relative placement of nucleotides
linked by a phosphodiester bond. However, it has already been
observed that distinct torsion angle combinations can result in
similar backbone directions and base orientations. This phenomenon is
known as the ``crankshaft effect'' [11,22]. Also,
non-adjacent base-base interactions, like base pairings that are
stabilized by H-bonds and non-adjacent base-base stacking, cannot be
accurately parameterized using these angles. Rather, a plethora of
rotation and translation parameters have been used to describe these
interactions [2,15,17]. A simplified
and unified encoding scheme for any type of base-base interactions
that emerged from the introduction of HTMs is introduced. In order to
allow us to effectively compare base-base interactions, a distance
metric between between two HTMs,
![]() and
and
![]() , should possess the following properties:
, should possess the following properties:
Equation 3.1 states that the distance metric should obviously be commutative. Equation 3.2 states that a relation should have a null distance with itself, but not with it's inverse unless they are equal. Equation 3.3 states that the distance metric should not depend on the direction of application, implicit in the HTM representation. The metric should allow us to discriminate non-directional nucleotide relations.
The simple Euclidean distance in the 16 dimensional space of HTMs does
not satisfy the above properties since HTMs embed a combination of
translation and rotation terms that need to be considered separately.
A HTM can be decomposed in the product of two HTMs,
![]() , where
, where ![]() contains the translation and
contains the translation and
![]() contains the rotation embedded in the original HTM.
Paul [23] showed how to extract the length of the
translation,
contains the rotation embedded in the original HTM.
Paul [23] showed how to extract the length of the
translation, ![]() , as well as the angle
, as well as the angle ![]() and the axis of
rotation
and the axis of
rotation ![]() from matrices
from matrices ![]() and
and ![]() . The
strength of a transformation,
. The
strength of a transformation, ![]() , regardless of the axis
of rotation, is defined by:
, regardless of the axis
of rotation, is defined by:
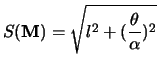 |
(3.4) |
Although HTMs are perfectly suited to uniformely encode base-base interactions, the information they contain is too compact to identify the type of relations they encode without reproducing the relation in 3-D space, and evaluating other parameters. For this reason, the symbolic annotations of base-base interactions are determined from atomic coordinates.